Materials Engineering

Mechanical Behavior of Metals

This is a very central topic:
What happens when we apply external forces to metals? If we stretch a spring too far, will it return to its original shape? No — it will experience permanent deformation.

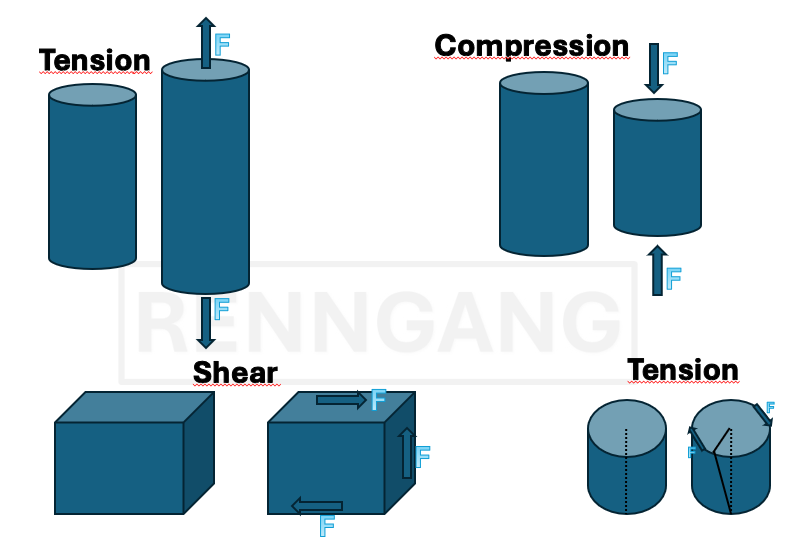the 915 Porsche Transmission, Trym Kongrød

We have different types of stresses:

Tensile stress (stretching)

Compressive stress (squeezing)

Shear stress, which acts in the plane of the cross-section

Torsion, which refers to twisting forces

We focus primarily on tensile and compressive stresses. These forces cause different types of deformation: either elastic (reversible) or plastic (permanent).

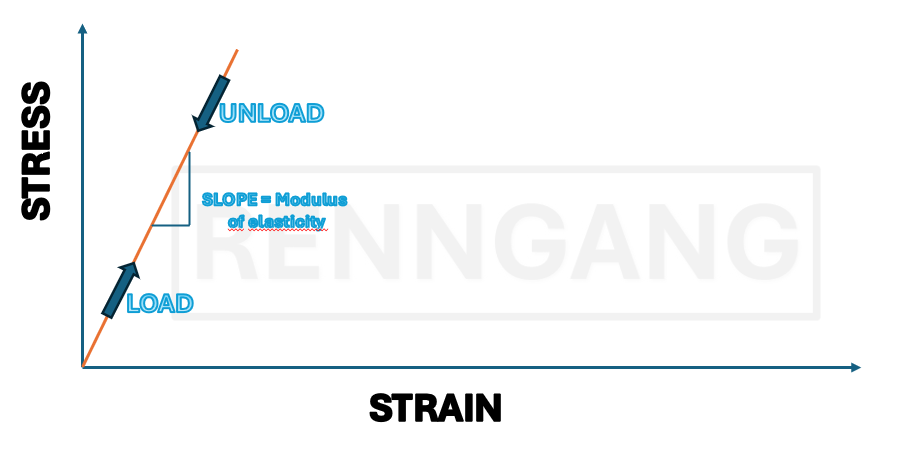
Elastic Deformation

Let’s begin by looking at elastic deformation. Imagine stretching a spring, it deforms, but the same thing happens down at the atomic level. When we stretch a crystalline material, its crystal structure is also stretched. This means that the atomic spacing within the crystal lattice increases correspondingly. As long as the deformation is elastic, the atomic bonds do not break, they remain intact.

A key characteristic of elastic deformation is that it is proportional to the applied force: If we double the force, we double the deformation. The material also returns to its original shape once the applied force is removed.

Hooke’s Law

The linear relationship between stress and strain is called Hooke’s Law.
We also have more general definitions for stress and strain:

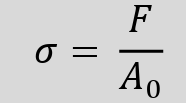Nominal stress is defined as the force divided by the original cross-sectional area of the material. As long as we use the original (unloaded) area, we refer to it as A₀, and this is usually what we apply in calculations—especially while the material behaves in the linear elastic region.

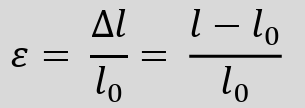Strain is defined as the change in length divided by the original length:
ε = ΔL / L₀

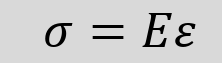The relationship between stress and strain, within the elastic region, is given by Hooke’s Law:
σ = E × ε
Where E is the Young’s modulus (or elastic modulus), which is a material-specific constant — often found in data tables. The modulus can also be determined experimentally through a tensile test, where stress is plotted against strain. The slope of the linear portion of the curve corresponds to the E-modulus.

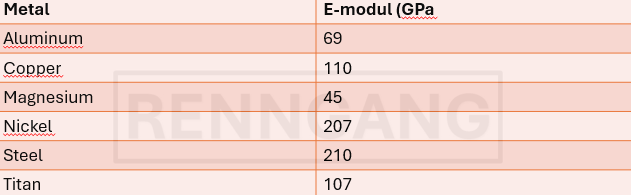Here we see the Young’s modulus for various metals. The unit is pascal (Pa), but since the values are large, it’s usually expressed in gigapascals (GPa). The E-modulus reflects the stiffness of a material — its resistance to elastic deformation under load.

Example Problem:

A copper rod with a length of 305 mm is subjected to a tensile stress of 276 MPa. Assuming elastic deformation, what is the elongation of the rod?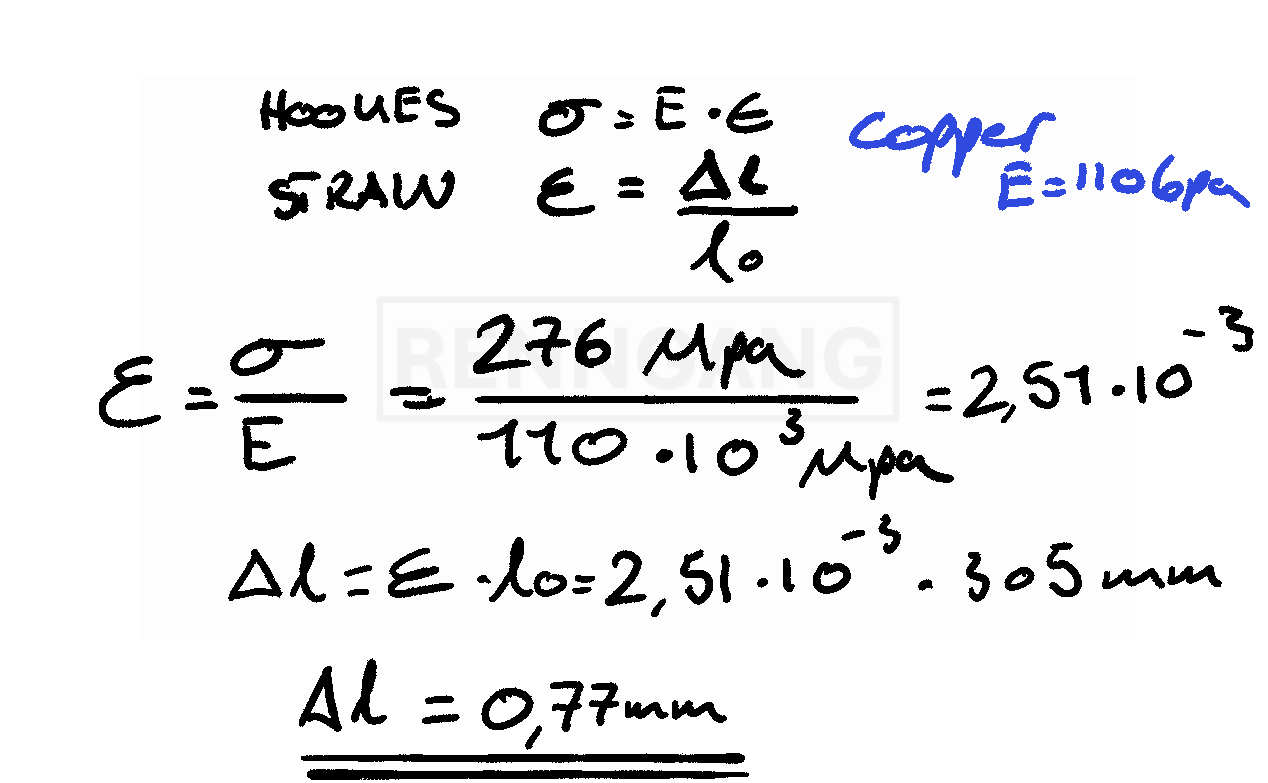

In problem-solving, we usually assume that the Young’s modulus (E-modulus) is constant — for example, at room temperature. But in reality, this is not always the case, as the modulus is actually temperature-dependent. This is because the E-modulus is essentially a measure of the bond strength within a material — that is, how strong the atomic bonds are. Therefore, different materials (and metals) have different E-moduli.

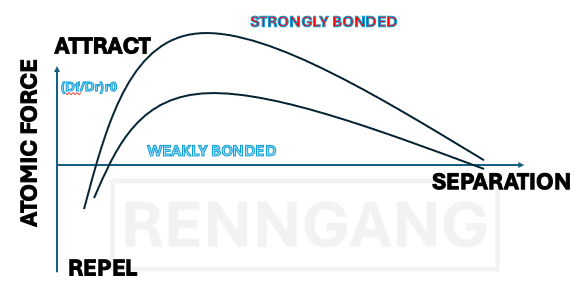The curve shown for the two metals in the figure illustrates how much force must be applied before deformation occurs.

A Bit About Shear Stress

The definition of shear stress is similar to that of tensile and compressive stress — it is also given as force per cross-sectional area. However, the difference lies in the direction of the force. In tension or compression, the force acts perpendicular to the cross-sectional area. In contrast, shear stress acts in the plane of the cross-section — parallel to it. Instead of elongating or compressing the material, shear stress causes a change in shape, known as shear deformation. If we imagine a cubic element, shear causes the right angle of the cube to distort. The angle by which it deforms is called the shear strain (γ). We can define a similar relationship between shear stress and shear strain — just like we did for tensile and compressive stress.

So, we also have a Hooke’s law for shear:
τ = G × γ,
where τ is shear stress, γ is shear strain, and G is the shear modulus.

Poisson’s Ratio

Poisson’s ratio describes the phenomenon that when we apply tensile forces to a material, it not only elongates, but also contracts laterally.
Poisson’s ratio expresses the relationship between longitudinal strain and lateral strain.

For example, if we stretch a cylindrical rod, Poisson’s ratio tells us how much the diameter decreases as a result of the applied tensile stress.

Longitudinal strain is given by the change in length divided by the original length.

Similarly, lateral strain is the change in width (or diameter) divided by the original width (or diameter).

Poisson’s ratio (ν) is then defined as the ratio of lateral strain to longitudinal strain:
ν = − (lateral strain) / (longitudinal strain)
The negative sign indicates that one dimension increases while the other decreases.

Example with tensile force

A tensile force is applied to a brass rod so that its diameter is reduced by 2.5 × 10⁻³ mm. The original diameter is 10 mm. How large must the tensile force F be?

Brass has:

A Young’s modulus (E) of 97 GPa

A Poisson’s ratio (ν) of 0.34.

Let’s walk through the steps to find the required tensile force F:

1) Find the lateral (transverse) strain

This is calculated as the change in diameter divided by the original diameter

2) Find the longitudinal (axial) strain

Use Poisson’s ratio

3) Use Hooke’s Law

To find the engineering stress (σ)

4) Finally, find the force F

Use the formula for stress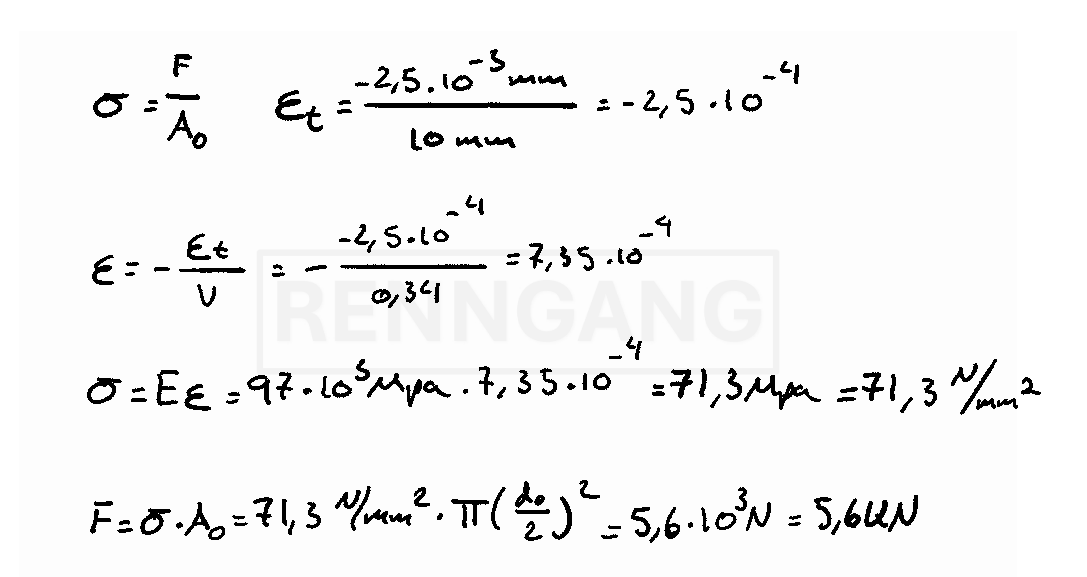

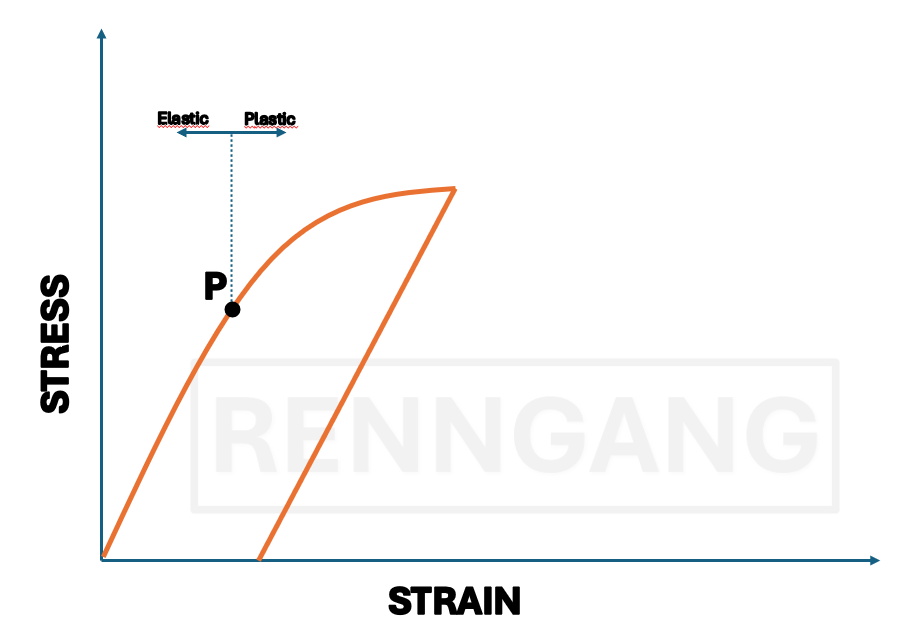
Plastic Deformation

Unlike elastic deformation, plastic deformation means that the material does not return to its original shape once the load is removed.
This curve shows how the deformation behaves when the load is removed.

Once we pass point P, the material can no longer return to its original length. The strain we read at the plastic strain point is the permanent deformation. We are particularly interested in the plastic properties of materials because many undergo plastic deformation during use.

A material’s ability to plastically deform is important for processes such as shaping, forging, rolling, and forming.
In many cases, the yield strength is used as the primary measure of the strength of a structural metal.

A Measure of Ductility

A key measure of ductility is how much plastic deformation a material can undergo before it fractures.
There are two common ways to assess this:

Elongation at break:

Measuring how much a test specimen elongates before fracture. This is called the fracture strain (also known as elongation at break).

Reduction of area:

Measuring how much the specimen necks (narrows) before it breaks. This is known as the fracture contraction or reduction in area.

Fracture strain can be read directly from a stress–strain curve, or measured from a physical specimen after testing.
It is calculated as:
(Change in length / Original length) × 100%

Reduction of area must be determined experimentally.

It cannot be observed from the stress–strain curve.
Instead, you measure the diameter of the test specimen before and after fracture and calculate the percentage reduction.

Brittle materials fracture much earlier — with little or no plastic deformation — compared to ductile materials.

Strength vs. Ductility

Strong metals often exhibit relatively low elongation at break.
Ductility can also be temperature-dependent.
For example, in iron, tensile tests performed at different temperatures demonstrate how ductility changes with temperature.

Resilience and Toughness

Resilience describes how much energy a material can absorb elastically.
It is represented by the area under the linear portion of the stress–strain curve (i.e., within the elastic region).
Toughness, on the other hand, refers to a material’s resistance to fracture in the presence of flaws such as microcracks or other defects.
It is a combination of strength and ductility.
Toughness is quantified by the total area under the entire stress–strain curve, from zero up to fracture.

Engineering Stress and Strain vs. True Stress and Strain

Engineering (Nominal) Stress and Strain:

Engineering stress is defined as the applied force (F) divided by the original cross-sectional area (A₀) of the specimen. This assumes the area remains constant throughout the deformation. It is commonly used in engineering calculations because it is simple and provides a practical overview.

• Engineering strain is defined as the relative change in length compared to the original length (L₀). This method does not account for the change in geometry or length during loading.

True Stress and Strain:

True stress accounts for the fact that the cross-sectional area (A) decreases during deformation (such as in tensile testing). It is defined as the applied force (F) divided by the instantaneous (current) area (A). True stress is always greater than engineering stress during tensile deformation because the area becomes smaller.

True strain considers that strain occurs incrementally. It is defined as the sum of small, instantaneous changes in length relative to the current length. This provides a more accurate description of deformation, especially for large strains.

Summary of Use:

Engineering (nominal) stress and strain are based on the original dimensions of the specimen. They offer a simplified approach that is often used in practical applications.

True stress and strain consider the changing dimensions of the specimen during loading. They provide a more realistic and precise description, particularly under large deformations.

In the elastic region, the difference between nominal and true values is small, so engineering values are often sufficient.

In the plastic region, where deformation is significant, true values are more accurate and preferred for analysis.